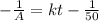Question

A 100-gallon barrel, initially half-full of oil, develops a leak at the bottom. Let A(t) be the amount of oil in the barrel at time t. Suppose that the amount of oil is decreasing at a rate proportional to the product of the time elapsed and the amount of oil present in the barrel. The mathematical model is:___________.

(a) =kA, A(0) = 0
(b) A = ktA, A(O) = 50
(c) A tA, A(0) = 100
(d) A = két +A), A
(e) = 50 None of the above.

Answer 1

the mathematical model is :
`-(1)/(A)= kt - (1)/(50)`

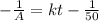
Explanation:

Given that:

Let A(t) to be the amount of oil in the barrel at time t.

However; Suppose that the amount of oil is decreasing at a rate proportional to the product of the time elapsed and the amount of oil present in the barrel.

Then,

`(dA)/(dt) \ \alpha \ A^2`

`(dA)/(dt)= KA^2`

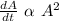
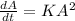
Initially the 100 -gallon barrel is half-full of oil

So, A(0) = 100/2 = 50

`(dA)/(dt)= KA^2 \ \ \ \ \ \ :A(0)=50`

The variable is now being separated as:

`(dA)/(A^2)=kdl`

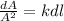
Taking integral of both sides; we have:

`\int\limits(dA)/(A^2)=\int\limits \ kdt`

`-(1)/(A)= kt +C`

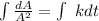
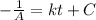
However; since A(0) = 50; Then

t = 0 ; A =50 in the above equation

`-(1)/(50)= 0 +C`

`C = - (1)/(50)`

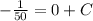
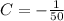
Thus; the mathematical model is :
`-(1)/(A)= kt - (1)/(50)`