Question

Researchers at a lake have determined that the percentage of fish in the lake that are intolerant to pollution can be estimated by the function

P(W,R,A)= 49-1.61W-1.41R-1.38A
where W is the percentage of wetland, R is the percentage of residential area, and A is the percentage of agricultural area surrounding the lake. Answer the questions below.
1.Use this function to estimate the percentage of fish that will be intolerant to pollution if 3 percent of the land is classified as wetland, 15 percent is classified as residential, and 0 percent is classified as agricultural.
(Note: The land can also be classified as forest land.)
2. What is the maximum percentage of fish that will be intolerant to pollution?
3. Which variable has the greatest influence on P W, R, or A

Answer 1

a. 23.02 %

b. 49%

c. W

Explanation:

Solution:-

- A multi-variable function for the percentage of fish in the lake that are intolerant to the pollution is given as:

`P ( W , R , A ) = 49 - 1.61W - 1.41R - 1.38A`

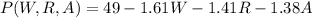
Where,

W: percentage of wetland

R: percentage of residential area

A: percentage of agriculture

- We are to evaluate the percentage of fish intolerant to pollution in the case where W = 3 , R = 15 , A = 0. We will plug in the values in the modeled function P ( W , R , A ) as follows:

`P ( 3 , 15 , 0 ) = 49 - 1.61*3 - 1.41*15 -1.38*0\\\\P ( 3 , 15 , 0 ) = 23.02\\`

- To determine the maximum percentage of fish that will be intolerant to pollution we will employ the use of critical points. The critical point that is defined by the linear relationship between P and all other parameters ( W, R , A ). The maximum value occurs when W = R = A = 0.

`P ( 0 , 0 , 0 ) = 49 - 1.61*0 -1.41*0 - 1.38*0 = 49`

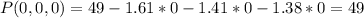
- Hence, the maximum value of the function is 49%.

- The linear relationship between each induvidual parameter ( R, W , A ) and the function ( P ) is proportional in influence. The extent of influence can be quantized by the constant multiplied by each parameter.

- We see that that ( 1.61*W ) > ( 1.41R ) > ( 1.38A ). The greatest influence is by parameter ( W ) i.e the influence of percentage of wetlands .