Question

Which first step for solving the given system using substitution results in an equation without fractions?

-9x4y - 10
-9x+3y3

Answer 1

Answer: solve for y in the second equation

Explanation:

I got it right on edenuity

Answer 2

The step to take to avoid fraction is to solve for y in equation 2

Explanation:

Given

-9x+ 4y =- 10

-9x+ 3y = 3

Required:

Step for solving using substitution (avoiding fraction)

Let -9x+ 4y =- 10 represent equation 1

and -9x+ 3y = 3 represent equation 2

The following points are to be noted

• Solving for x or y in equation 1 will definitely lead to having fractions

• Solving for x in equation 2 will also lead to having fractions

Having said that, the step to take to avoid fraction is to solve for y in equation 2

Check

`-9x+ 3y = 3`

Add 9x to both sides

`9x-9x+ 3y = 3 + 9x`

`3y = 3 + 9x`

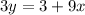
Divide through by 3

`(3y)/(3) = (3 + 9x)/(3)`

`y = (3 + 9x)/(3)`

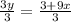
Split fraction

`y = (3)/(3) + (9x)/(3)`

`y = 1 + 3x`

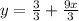
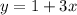
At the point, the expression of y can then be substituted in equation 1