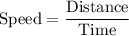Question

"Opportunity" and "Phoenix" are two of the robotic explorers on Mars. Opportunity landed at 2° south latitude, where Mars’ radius is about 2110 miles. Phoenix landed at 68° north latitude, where Mars’ radius is about 790 miles. Mars rotates on its axis once every 24.6 Earth-hours. How far does each explorer travel as Mars rotates by 1 radian? How many hours does it take Mars to rotate 1 radian? Using this answer, how fast is each explorer traveling around Mars’ axis in miles per hour?

Answer 1

(a)Distance traveled by each explorer travel as Mars rotates by 1 radian

• Opportunity=2108.71 miles

• Phoenix =295.94 miles

(b)Number of hours it takes Mars to rotate 1 radian=3.9152 hours

(c)Speed of each explorer around Mars.

• Opportunity=538.59 miles per hour
• Phoenix =75.59 miles per hour

Explanation:

Part A

For any given parallel of latitude
`\text{Circumference}=2\pi R \cos \beta$ where \beta$ is the angle of latitude.`

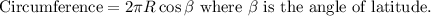
Opportunity landed at 2° south latitude, where Mars’ radius is about 2110 miles.

`\text{Circumference at 2\°S latitude}=2\pi*2110* \cos 2^\circ\\=13249.44$ miles`

Phoenix landed at 68° north latitude, where Mars’ radius is about 790 miles.

`\text{Circumference at 68\°N latitude}=2\pi*790* \cos 68^\circ\\=1859.44$ miles`

Part B

Next, we determine the distance (Length of arc) covered by each explorer as Mars rotates by 1 radian.

`\text{Length of arc (in radian)}=(\theta)/(2\pi) * $Circumference`

Opportunity's Distance

`=(1)/(2\pi) * 13249.44\\\\ =2108.71$ miles`

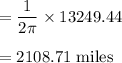
Phoenix's Distance

`=(1)/(2\pi) * 1859.44\\\\ =295.94$ miles`

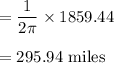
Part C

Mars rotates on its axis once every 24.6 Earth-hours.

Therefore:

`(24.6)/(2\pi) \approx $ 3.9152 hour per radian`

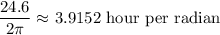
Part D:Speed of each explorer

`\text{Speed}=\frac{\text{Distance}}{\text{Time}}`

`\text{Speed of Opportunity = }(2108.71)/(3.9152)\\$=538.59 miles per hour\\\\Speed of Phoenix =(295.94)/(3.9154)\\=75.59$ miles per hour`