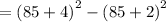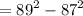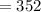Question

Three consecutive positive odd integers a, b and c satisfy b^2 - a^2 = 344 and c^2 - b^2 > 0. What is the value of c^2 - b^2?

Answer 1

The value of c² - b² is 352.

Explanation:

Given that a, b and c are consecutive odd number. In a simplier way, you can make an expression of b and c in terms of a, as b and c are consecutive numbers which are connected to a :

`let \: a = a \\ let \: b = a + 2 \\ let \: c = a + 2 + 2 = a + 4`

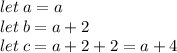
e.g

Let a = 1,

b = a + 2

= 1 + 2

= 3 (odd number)

c = a + 4

= 1 + 4

= 5 (odd number)

Then, substitite the expression of a and b into b² - a² = 344, in order to find a :

`{b}^(2) - {a}^(2) = 344`

`{(a + 2)}^(2) - {a}^(2) = 344`

`{a}^(2) + 4a + 4 - {a}^(2) = 344`

`4a + 4 = 344`

`4a = 340`

`a = 85`

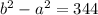
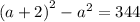
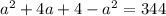
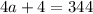
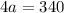
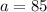
Next, we have to substitute the value of a into the expression c² - b² :

`{(a + 4)}^(2) - {(a + 2)}^(2)`

`= {(85 + 4)}^(2) - {(85 + 2)}^(2)`

`= {89}^(2) - {87}^(2)`

`= 352`