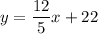Answer:
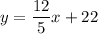
Explanation:
Slope-intercept form of line:
First find the slope of the line AB. ie, m
Slope of the perpendicular line = -1/m
(2 , 3) ⇒ x₁ = 2 & y₁ = 3
(-10, 8) ⇒ x₂ = -10 & y₂ = 8
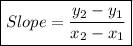
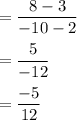

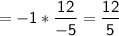
Equation of the required line: y = mx + b
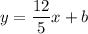
The line passes through (-5 , 10). Substitute in the above equaiton,
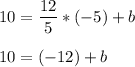
10 + 12 = b
b = 22
Equation of the line: