Answer:
47.5% of students fall within heights of 100 cm to 120 cm
Explanation:
We are given that heights of Grade 1 students are normally distributed
Mean =
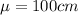
Standard deviation =
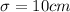
a)
Empirical rule
68% of data lies within the first standard deviation from the mean i.e
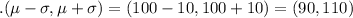
95% of all the data will fall within two standard deviations i.e.
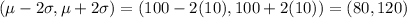
99.7% of data lies within the three standard deviations i.e.
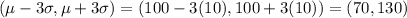
b)Percentage of students fall within heights of 100 cm to 120 cm
Using the normal distribution curve
Percentage of students fall within heights of 100 cm to 120 cm =
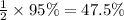
Hence 47.5% of students fall within heights of 100 cm to 120 cm