Answer:
Step-by-step explanation:
Given that :
the diameter of the reservoir D = 18 mm
the diameter of the manometer d = 6 mm
For an equilibrium condition ; the pressure on both sides are said to be equal
∴

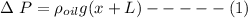
According to conservation of volume:
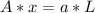
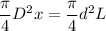
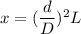
Replacing x into (1) ; we have;
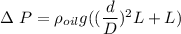
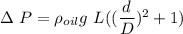

Thus; the liquid deflection is :

when the applied pressure is equivalent to 25 mm of water (gage); the liquid deflection is:

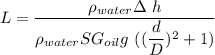
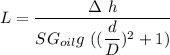
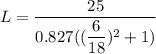
L = 27.21 mm