Answer:
The kinetic energies just before touching the ground are as follows;
Case 1
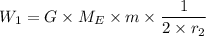
Case 2
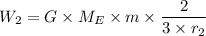
The correct option is;
K2 = (4/3) K1
Step-by-step explanation:
The work done is given by the relation;
For case 1
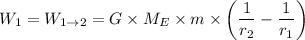
Where for case 1 we have:
G = Gravitational constant = 6.67408 × 10⁻¹¹ m³/(kg·s²)
r₂ = Radius of the Earth
r₁ = 2 × Radius of the Earth = 2 × r₂
Hence;
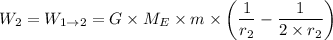
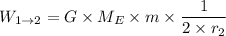
For case 2 we have:
G = Gravitational constant = 6.67408 × 10⁻¹¹ m³/(kg·s²)
r₂ = Radius of the Earth
r₁ = 3 × Radius of the Earth = 2 × r₂
Hence;
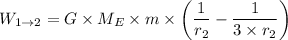
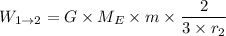
Therefore;
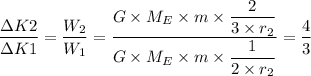
Hence;
K2 = (4/3) × K1.