Complete Question
An isolated charged soap bubble of radius R0 = 7.45 cm is at a potential of V0=307.0 volts. V0=307.0 volts. If the bubble shrinks to a radius that is 19.0%19.0% of the initial radius, by how much does its electrostatic potential energy ????U change? Assume that the charge on the bubble is spread evenly over the surface, and that the total charge on the bubble r
Answer:
The difference is

Step-by-step explanation:
From the question we are told that
The radius of the soap bubble is

The potential of the soap bubble is
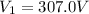
The new radius of the soap bubble is
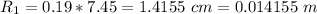
The initial electric potential is mathematically represented as
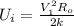
The final electric potential is mathematically represented as
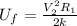
The initial potential is mathematically represented as
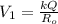
The final potential is mathematically represented as
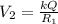
Now
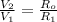
substituting values
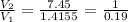
=>
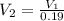
So

Therefore
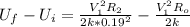
![U_f -U_i = (V_1^2)/(2k) [( R_1 )/( * 0.19^2) - R_o]](https://img.qammunity.org/2021/formulas/physics/college/fl3mfh1xgqoitcucf8xabn6wb1rdawmq7k.png)
where k is the coulomb's constant with value
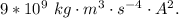
substituting values
![U_f -U_i = (307^2)/(9 * 10^(9)) [( 0.014155 )/( 0.19^2) - 0.0745]](https://img.qammunity.org/2021/formulas/physics/college/5z3pes9chj1rxlspl97n7c7qmsmvicou3o.png)
