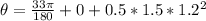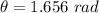Complete Question
In testing an automobile tire for proper alignment, a technician marks a spot on the tire 0.190 m from the center. He then mounts the tire in a vertical plane and notes that the radius vector to the spot is at an angle of 33.0° with the horizontal. Starting from rest, the tire is spun rapidly with a constant angular acceleration of 1.50 rad/s2. (Assume the spot's position is initially positive, and assume the angular acceleration is in the positive direction.)
(a) What is the angular speed of the wheel after 1.20 s? rad/s
b) What is the tangential speed of the spot after 1.20 s?
(c) What is the magnitude of the total acceleration of the spot after 1.20 s?
(d) What is the angular position of the spot after 1.20 s?
Answer:
a

b
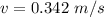
c
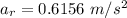
d
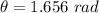
Step-by-step explanation:
From the question we are told that
The distance of the spot from the center is
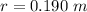
The angle of the radius vector with the horizontal is
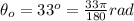
The acceleration is
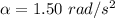
The angular speed of the wheel after 1.20 s is mathematically represented as
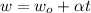
Where
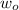 is the initial angular speed of the wheel which is zero
is the initial angular speed of the wheel which is zero
Substituting values
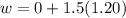

the tangential speed of the spot after 1.20 is mathematically represented as
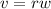
substituting values

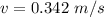
The magnitude of the total acceleration of the spot after 1.30 s is mathematically represented as
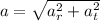
The radial acceleration is

substituting values
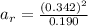
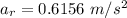
The tangential acceleration is
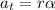
substituting values
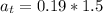
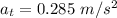
=>

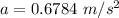
the angular position of the spot after 1.20 s is mathematically represented as
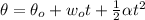
substituting values