Question

A spherical shell contains three charged objects. The first and second objects have a charge of −18.0 nC−18.0 nC and 38.0 nC38.0 nC , respectively. The total electric flux through the shell is −218 N⋅m2/C−218 N⋅m2/C . What is the charge on the third object?

Answer 1

q3 = 21.9 nC

Step-by-step explanation:

By the Gauss theorem you have that the electric flux in a Gaussian surface is given by:

`\Phi_E=(Q)/(\epsilon_o)` (1)

ФE: electric flux = -218Nm^2/C

Q: net charge inside the Gaussian surface

εo: dielectric permittivity of vacuum = 8.85*10^-12 C^2/(Nm^2)

You can consider the spherical shell as a Gaussian surface. Then, the net charge inside the surface is:

`Q=-18.0nC+38.0nC+q_3` (2)

where charge q3 is unknown charge of the third object:

You replace the equation (2) into the equation (1), and you solve for q3:

`\epsilon_0 \Phi_E=-18.0*10^(-9)C+38.0*10^(-9)C+q_3\\\\\epsilon_0 \Phi_E=20*10^(-9)C+q_3\\\\q_3=(8.85*10^(-12)C^2/(Nm^2))(-218Nm^2/C)-20*10^(-9)C\\\\q_3=2.19*10^(-9)C=21.9nC`

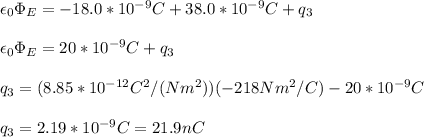
hence, the charge of the third object is 21.9 nC