Answer:
Explanation:
Hello!
X₁: speed of a motorcycle at a certain intersection.
n₁= 135
X[bar]₁= 33.99 km/h
S₁= 4.02 km/h
X₂: speed of a car at a certain intersection.
n₂= 42 cars
X[bar]₂= 26.56 km/h
S₂= 2.45 km/h
Assuming
X₁~N(μ₁; σ₁²)
X₂~N(μ₂; σ₂²)
and σ₁² = σ₂²
A 90% confidence interval for the difference between the mean speeds, in kilometers per hour, of motorcycles and cars at this intersection is ________.
The parameter of interest is μ₁-μ₂
(X[bar]₁-X[bar]₂)±
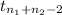 *
*
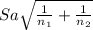
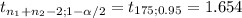
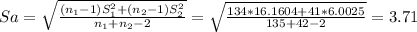
[(33.99-26.56) ± 1.654 *(
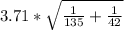 )]
)]
[6.345; 8.514]= [6.35; 8.51]km/h
Construct the 98% confidence interval for the difference μ₁-μ₂ when X[bar]₁= 475.12, S₁= 43.48, X[bar]₂= 321.34, S₂= 21.60, n₁= 12, n₂= 15
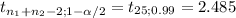
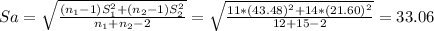
[(475.12-321.34) ± 2.485 *(
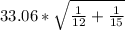 )]
)]
[121.96; 185.60]
I hope this helps!