Question

Traffic speed: The mean speed for a sample of cars at a certain intersection was kilometers per hour with a standard deviation of kilometers per hour, and the mean speed for a sample of motorcycles was kilometers per hour with a standard deviation of kilometers per hour. Construct a confidence interval for the difference between the mean speeds of motorcycles and cars at this intersection. Let denote the mean speed of motorcycles and round the answers to at least two decimal places. A confidence interval for the difference between the mean speeds, in kilometers per hour, of motorcycles and cars at this intersection is ________.

Construct the 98% confidence interval for the difference μ 1-y 2 when x 1 475.12, x 2-32134, s 1-43.48, s 2-21.60, n 1-12, and n 2-15. Use tables to find the critical value and round the answers to two decimal places. A 98% confidence interval for the difference in the population means is ________.

Answer 1

Explanation:

Hello!

X₁: speed of a motorcycle at a certain intersection.

n₁= 135

X[bar]₁= 33.99 km/h

S₁= 4.02 km/h

X₂: speed of a car at a certain intersection.

n₂= 42 cars

X[bar]₂= 26.56 km/h

S₂= 2.45 km/h

Assuming

X₁~N(μ₁; σ₁²)

X₂~N(μ₂; σ₂²)

and σ₁² = σ₂²

A 90% confidence interval for the difference between the mean speeds, in kilometers per hour, of motorcycles and cars at this intersection is ________.

The parameter of interest is μ₁-μ₂

(X[bar]₁-X[bar]₂)±
`t_(n_1+n_2-2)` *
`Sa\sqrt{(1)/(n_1) +(1)/(n_2) }`

`t_(n_1+n_2-2;1-\alpha /2)= t_(175; 0.95)= 1.654`

`Sa= \sqrt{((n_1-1)S_1^2+(n_2-1)S_2^2)/(n_1+n_2-2) } = \sqrt{(134*16.1604+41*6.0025)/(135+42-2) } = 3.71`

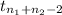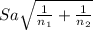
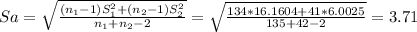
[(33.99-26.56) ± 1.654 *(
`3.71*\sqrt{(1)/(135) +(1)/(42) }`)]

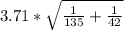[6.345; 8.514]= [6.35; 8.51]km/h

Construct the 98% confidence interval for the difference μ₁-μ₂ when X[bar]₁= 475.12, S₁= 43.48, X[bar]₂= 321.34, S₂= 21.60, n₁= 12, n₂= 15

`t_(n_1+n_2-2;1-\alpha /2)= t_(25; 0.99)= 2.485`

`Sa= \sqrt{((n_1-1)S_1^2+(n_2-1)S_2^2)/(n_1+n_2-2) } = \sqrt{(11*(43.48)^2+14*(21.60)^2)/(12+15-2) } = 33.06`

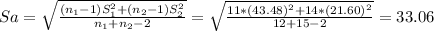
[(475.12-321.34) ± 2.485 *(
`33.06*\sqrt{(1)/(12) +(1)/(15) }`)]

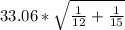[121.96; 185.60]

I hope this helps!