Answer:
3.2 ft
Explanation:
The initial distance from the base of the ladder to the wall is:
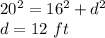
After moving the ladder, the distance from the base to the wall is 12 - 2x while the height of the ladder is 16 + x. The distance x is given by:
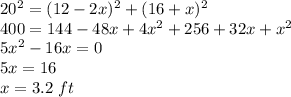
Therefore, the top of the ladder is 3.2 ft higher now.