Question

Steam reforming of methane (CH4 ) produces "synthesis gas," a mixture of carbon monoxide gas and hydrogen gas, which is the starting point for many important industrial chemical syntheses. An industrial chemist studying this reaction fills a tank with of methane gas and of water vapor, and when the mixture has come to equilibrium measures the amount of carbon monoxide gas to be 18 mol . Calculate the concentration equilibrium constant for the steam reforming of methane at the final temperature of the mixture. Round your answer to significant digits.

Answer 1

The question is incomplete, here is the complete question:

Steam reforming of methane
`(CH_4)` produces "synthesis gas," a mixture of carbon monoxide gas and hydrogen gas, which is the starting point for many important industrial chemical syntheses. An industrial chemist studying this reaction fills a 125 L tank with 20 mol of methane gas and 10 mol of water vapor at 38 degrees celsius. He then raises the temperature, and when the mixture has come to equilibrium measures the amount of hydrogen gas to be 18 mol . Calculate the concentration equilibrium constant for the steam reforming of methane at the final temperature of the mixture. Round your answer to significant digits.

Answer: The equilibrium constant for the reaction is
`3.99* 10^(-2)`

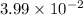
Step-by-step explanation:

We are given:

Initial moles of methane gas = 20 moles

Initial moles of water vapor = 10 moles

Equilibrium moles of carbon monoxide = 18 moles

Volume of the tank = 125 L

The chemical equation for the reaction of methane and water vapor follows:

`CH_4(g)+H_2O(g)\rightleftharpoons CO(g)+3H_2(g)`

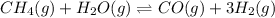
Initial: 20 10

At eqllm: 20-x 10-x x 3x

Evaluating the value of 'x':

`\Rightarrow 3x=18\\x=6`

So, equilibrium moles of methane gas = (20 - x) = [20 - 6] = 14 mol

Equilibrium moles of water vapor = (10 - x) = [10 - 6] = 4 mol

Equilibrium moles of carbon monoxide gas = x = 6 mol

The expression of equilibrium constant for the above reaction follows:

`K_(eq)=([H_2]^3[CO])/([CH_4][H_2O])`

We are given:

`[H_2]=(18)/(125)=0.144M`

`[CO]=(6)/(125)=0.048M`

`[CH_4]=(14)/(125)=0.112M`

`[H_2O]=(4)/(125)=0.032M`

Putting values in above expression, we get:

`K_(eq)=((0.144)^3* 0.048)/(0.112* 0.032)\\\\K_(eq)=3.99* 10^(-2)`

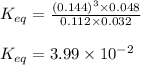
Hence, the equilibrium constant for the reaction is
`3.99* 10^(-2)`