Question

A ball is kicked at an angle of 35° with the ground.a) What should be the initial velocity of the ball so that it hits a target that is 30 meters away at a height of 1.8 meters?b) What is the time for the ball to reach the target?

Answer 1

a.18.5 m/s

b.1.98 s

Step-by-step explanation:

We are given that

`\theta=35^(\circ)`

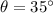
a.Let
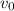`v_0` be the initial velocity of the ball.

Distance,x=30 m

Height,h=1.8 m

`v_x=v_0cos\theta=v_0cos35`

`v_y=v_0sin\theta=v_0sin35`

`x=v_0cos\theta* t=v_0cos35* t`

`t=(30)/(v_0cos35)`

`h=v_yt-(1)/(2)gt^2`

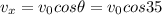
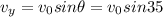
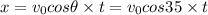
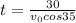
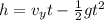
Substitute the values

`1.8=v_0sin35(30)/(v_0cos35)-(1)/(2)(9.8)((30)/(v_0cso35))^2`

`1.8=30tan35-(6574.6)/(v^2_0)`

`(6574.6)/(v^2_0)=21-1.8=19.2`

`v^2_0=(6574.6)/(19.2)`

`v_0=\sqrt{(6574.6)/(19.2)}=18.5 m/s`

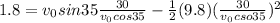
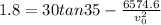
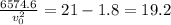
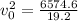
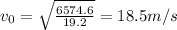
Initial velocity of the ball=18.5 m/s

b.Substitute the value then we get

`t=(30)/(18.5cos35)`

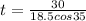
t=1.98 s

Hence, the time for the ball to reach the target=1.98 s