Question

Find the critical points and phase portrait of the differential equation below. Classify each critical point as stable, unstable, or semi-stable. By hand, sketch typical solution curves in the regions in the xy-plane determined by the graphs of the equilibrium solutions. Show work to verify your arrow directions in each interval.

dy/dx = y4 - 6y3 +8y2

Answer 1

The critical points are 0,2,4

0 is semi-stable, 2 is stable, 4 is unstable.

Check the phase line and the solution curves in the files attached below

Explanation:

`dy/dx = y^(4) - 6y^(3) + 8y^(2)`

To get the critical points, dy/dx = 0

`y^(4) - 6y^(3) + 8y^(2) = 0\\y^(2) ( y^(2) - 6y + 8) = 0\\y^(2) ( y-2)(y-4) = 0\\y = 0, 2, 4`

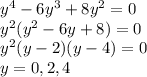
To classify the stability, the interval
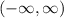`(-\infty, \infty)` is divided into
`(-\infty, 0), (0,2), (2,4),(4, \infty)`

`f(y) = y^(4) - 6y^(3) +8y^(2)`

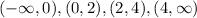
If y = -1, f(-1) = 15 > 0

If y = 1, f(1) = 3 > 0

If y = 3, f(3) = -9 < 0

If y = 5, f(5) = 75 > 0

The phase line is drawn in the file attached.

By critically observing the phase line:

The point y = 4 is unstable because the arrows are moving away from it

The point y = 2 is stable because the arrows are moving towards it

The point y = 0 is semi-stable because one arrow is moving towards it while the other moves away from it.

The typical solution curves are sketched in the file attached below.