Complete and clearly written Question:
A firm has two plants that produce identical output. The cost functions are:
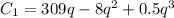 and
and
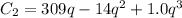 . At what output level does the average cost curve of each plant reach its minimum?
. At what output level does the average cost curve of each plant reach its minimum?
Answer:
The first price reaches minimum average at 8 units of outputs
The second price reaches minimum average at 7 units of outputs
Step-by-step explanation:
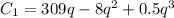

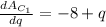
At minimum price,
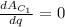
-8 + q = 0
q = 8
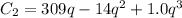
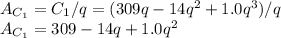
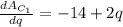
At minimum price,
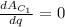
-14 + 2q = 0
2q = 14
q = 7