Question

A football quarterback has two more chances to throw a touchdown before his team is forced to punt the ball. He misses the receiver on the first throw 25% of the time. When his first throw is incomplete, he misses the receiver on the second throw 15% of the time. What is the probability of not throwing the ball to a receiver on either throw?

Answer 1

3.75%

Explanation:

the user above explains it very well

Answer 2

3.75% probability of not throwing the ball to a receiver on either throw

Explanation:

We use the conditional probability formula to solve this question. It is

`P(B|A) = (P(A \cap B))/(P(A))`

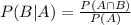
In which

P(B|A) is the probability of event B happening, given that A happened.

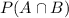`P(A \cap B)` is the probability of both A and B happening.

P(A) is the probability of A happening.

What is the probability of not throwing the ball to a receiver on either throw?

The throws are independent of each other.

Event A: Missing the first throw.

Event B: Missing the second throw.

He misses the receiver on the first throw 25% of the time.

This means that P(A) = 0.25

When his first throw is incomplete, he misses the receiver on the second throw 15% of the time.

This means that P(B|A) = 0.15

Then

`P(B|A) = (P(A \cap B))/(P(A))`

`P(A \cap B) = P(A)P(B|A) = 0.25*0.15 = 0.0375`

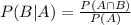
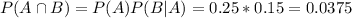
3.75% probability of not throwing the ball to a receiver on either throw