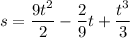Question

during each cycle, the velocity v (in meters per second) of a robotic welding device is given by v=9t-2/9+t^2, where t is time in seconds. find the expression for the displacement s (in meters) as a function of t if s=0 when t=0.​

Answer 1

`d = (9t^(2) )/(2) - (2)/(9) t + (t^3)/(3)`

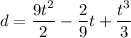
Explanation:

Given the equation of velocity w.r.to time 't':

`v=9t-(2)/(9)+t^2 ...... (1)`

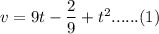
Formula for Displacement:

`Displacement = \text{velocity} * \text{time}`

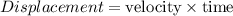
So, if we find integral of velocity w.r.to time, we will get displacement.

`\Rightarrow \text{Displacement}=\int {v} \, dt`

`\Rightarrow \int {v} \, dt = \int ({9t-(2)/(9)+t^2}) \, dt \\\Rightarrow \int{9t} \, dt - \int{(2)/(9)} \, dt + \int{t^2} \, dt\\\Rightarrow s=(9t^(2) )/(2) - (2)/(9) t + (t^3)/(3) + C ....... (1)`

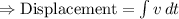
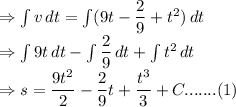
Here, C is constant (because it is indefinite integral)

Formula for integration used:

`1.\ \int({A+B}) \, dx = \int {A} \, dx + \int{B} \, dx \\2.\ \int({A-B}) \, dx = \int {A} \, dx - \int{B} \, dx \\3.\ \int{x^(n) } \, dx = (x^(n+1))/(n+1)\\4.\ \int{C } \, dx = Cx\ \{\text{C is a constant}\}`

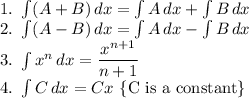
Now, it is given that s = 0, when t = 0.

Putting the values in equation (1):

`0=(9* 0^(2) )/(2) - (2)/(9)* 0 + (0^3)/(3) + C\\\Rightarrow C = 0`

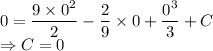
So, the equation for displacement becomes:

`s=(9t^(2) )/(2) - (2)/(9) t + (t^3)/(3)`