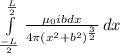Answer:
b. μ0I/4π∫ dx b/(b2 + x2)³/² j
Step-by-step explanation:
The wire of length L centered at origin ( x =0 and y=0 ) carries current of I . We have to find magnetic field at point ( x = 0 , y = b ) .
First of all we shall consider magnetic field due to current element idx which is at x distance away from origin . magnetic field
dB =
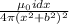
component of magnetic field along y- axis at point P
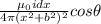
where θ is angle between y - axis and dE .
component of magnetic field along y- axis at point P
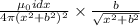
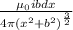
The same magnetic field will also exist due to current element dx at x distance away on negative x - axis
The perpendicular component will cancel out .
This is magnetic field dE due to small current element
Magnetic field due to whole wire