Answer:
 = 28800 Pa or 28.8 kPa
= 28800 Pa or 28.8 kPa
Step-by-step explanation: To determine the pressure of a liquid in a rotating tank,it is used:
p =
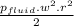 - γfluid . z + c
- γfluid . z + c
where:
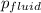 is the liquid's density
is the liquid's density
w is the angular velocity
r is the radius
γfluid.z is the pressure variation due to centrifugal force.
For this question, the difference between a point on the circumference and a point on the axis will be:
 =
=
 - γfluid.
- γfluid.
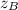 - (
- (
 - γfluid.
- γfluid.
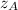 )
)
 =
=
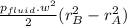 - γfluid(
- γfluid(
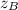 -
-
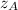 )
)
Since there is no variation in the z-axis, z = 0 and that the density of oil is 0.9.10³kg/m³:
 =
=
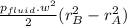

 = 28800
= 28800
The difference in pressure between two points, one on the circumference and the other on the axis is
 = 28800 Pa or 28.8 kPa
= 28800 Pa or 28.8 kPa