Answer:
The reasonable range for the population mean is (61%, 75%).
Explanation:
The interval estimate of a population parameter is an interval of values that consist of the values within which the true value of the parameter lies with a certain probability.
The mean of the sampling distribution of sample proportion is,
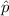 .
.
One of the best interval estimate of population proportion is the 95% confidence interval for proportion,
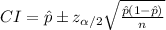
Given:
n = 150
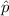 = 0.68
= 0.68
The critical value of z for 95% confidence level is:
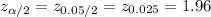
Compute the 95% confidence interval for proportion as follows:
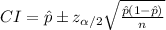

Thus, the reasonable range for the population mean is (61%, 75%).