Question

A right prism has bases that are isosceles trapezoids which have sides of length 16, 25, 25, and 30. The volume of the prism is 5520. What is the surface area?

Answer 1

2064 Square Units

Explanation:

First, we determine the height of the Isosceles Trapezoid

From the first diagram. the right triangle formed has a base length of 7 units and hypotenuse of 25 units.

Using Pythagoras Theorem

`25^2=7^2+h^2\\h^2=25^2-7^2\\h^2=576\\h^2=24^2\\h=24$ units`

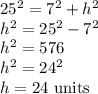
Height of the Trapezoid =24 units

Area of a trapezoid
`=(1)/(2)(a+b)h`

`=(1)/(2)(16+30)*24\\=552$ square units`

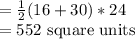
Therefore:

Base Area of the Prism =552 square units

Volume of a Prism =Base Area X Length

5520 =552 X Length

Length of the Prism =10 Units

Therefore:

Surface Area of the Prism = 2(Area of Isosceles trapezoid)+Area of 4 Rectangles

From the second diagram. the rectangles formed are of dimensions:

• 30 by 10
• 10 by 25
• 10 by 25; and
• 16 by 10

Surface Area of the Prism = 2(552)+(30X10)+(10X25)+(10X25)+(10X16)

=1104+300+250+250+160

=2064 Square Units