Answer:
Explanation:
Given that
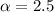 ,
,
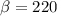
The weibull distribution with parameters
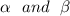
where
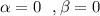
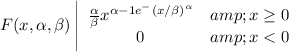
Then,

A) The probability that a specimen's lifetime is at most 250 is

The probability that the specimen's life time is more than 300 is
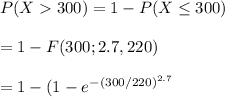

= 0.0992
b)The probability of the specimen's lifetime is between 100 and 250
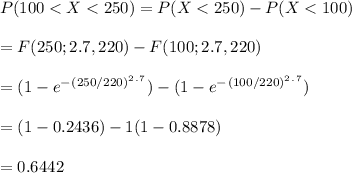
c) The value such that exactly 50% of all specimens have lifetimes exceeding that value is
![P(X>x)=0.50\\\\1-P(X<x)=0.50\\\\1-(1-e^-^{(x/220)^(2.7)}=0.50\\\\e^-^{(x/220)^(2.7)}=0.50\\\\-(x/220)^(2.7)=In(0.50)\\\\(x/220)^(2.7)=-In(0.50)\\\\(x/220)=[-In(0.50)]^{((1)/(2.7))} \\\\x=220[-In(0.50)]^{((1)/(2.7))}](https://img.qammunity.org/2021/formulas/mathematics/college/gufq77nt11lhf366pwuecw5iw5sasy37ra.png)
x = 192.07