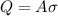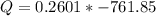Answer:
a)
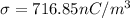
b)
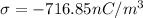
c) i)
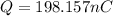
ii)
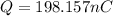
Step-by-step explanation:
To find the charge density on each face, let's use the formula: E=σ/εo
Where, E, electric field = 81.0 kN/C
εo =
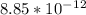
Thus, solve for σ
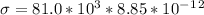
 or
or
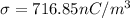
In charge density, the left face is negative while on the right face it will be positive.
Therefore,
Charge density on the each face =
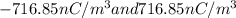
C) We'll first find the area of the square plate.
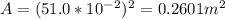
Use the formula below to find the magnitude of the charge on each surface of the plate:
On the right surface:
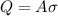

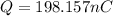
On the left surface: