Answer:
a) v = 1524.7 m/s
b) T = 8.47*10^-4 s
λ = 1.29 m
Step-by-step explanation:
a) First, in order to calculate the speed of the sound wave, you take into account that the velocity is constant, then, you use the following formula:
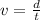
d: distance traveled by the sound wave, which is twice the distance to the ocean bottom = 2*324 m = 648 m
t: time that sound wave takes to return to the sub = 0.425
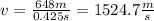
hence, the speed of the sound wave is 1524.7 m/s
b) Next, with the value of the velocity of the wave you can calculate the wavelength of the wave, by using the following formula:
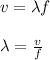
f: frequency = 1.18*10^3 Hz
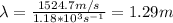
And the period is:
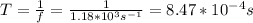
hence, the wavelength and period of the sound wave is, respectively, 1.29m and 8.47*10^-4 s