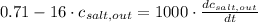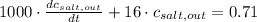Question

A tank is filled with 1000 liters of pure water. Brine containing 0.04 kg of salt per liter enters the tank at 9 liters per minute. Another brine solution containing 0.05 kg of salt per liter enters the tank at 7 liters per minute. The contents of the tank are kept thoroughly mixed and the drains from the tank at 16 liters per minute. A. Determine the differential equation which describes this system. Let S(t)S(t) denote the number of kg of salt in the tank after tt minutes. Then

Answer 1

The differential equation which describes the mixing process is
`(dc_(salt,out))/(dt) + (2)/(125)\cdot c_(salt,out) = (71)/(100000)`.

Explanation:

The mixing process within the tank is modelled after the Principle of Mass Conservation, which states that:

`\dot m_(salt,in) - \dot m_(salt,out) = (dm_(tank))/(dt)`

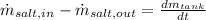
Physically speaking, mass flow of salt is equal to the product of volume flow of water and salt concentration. Then:

`\dot V_(water, in, 1)\cdot c_(salt, in,1) + \dot V_(water, in, 2) \cdot c_(salt,in, 2) - \dot V_(water, out)\cdot c_(salt, out) = V_(tank)\cdot (dc_(salt,out))/(dt)`

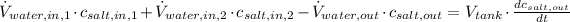
Given that
`\dot V_(water, in, 1) = 9\,(L)/(min)`,
`\dot V_(water, in, 2) = 7\,(L)/(min)`,
`c_(salt,in,1) = 0.04\,(kg)/(L)`,
`c_(salt, in, 2) = 0.05\,(kg)/(L)`,
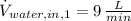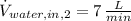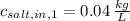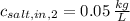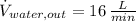`\dot V_(water, out) = 16\,(L)/(min)` and
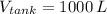`V_(tank) = 1000\,L`, the differential equation that describes the system is:

`0.71 - 16\cdot c_(salt,out) = 1000\cdot (dc_(salt,out))/(dt)`

`1000\cdot (dc_(salt, out))/(dt) + 16\cdot c_(salt, out) = 0.71`

`(dc_(salt,out))/(dt) + (2)/(125)\cdot c_(salt,out) = (71)/(100000)`