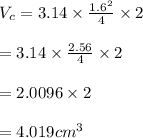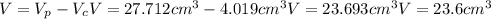Question

A steel hex nut has two regular hexagonal bases and a cylindrical hole with a diameter of 1.6 centimeters through the middle. The apothem of the hexagon is 2 centimeters. A cylinder is cut out of the middle of a hexagonal prism. The hexagon has an apothem with a length of 2 centimeters and base side lengths of 2.3 centimeters. The prism has a height of 2 centimeters. The cylinder has a diameter of 1.6 centimeters. The equation for the area of a regular hexagon = one-half (apothem) (perimeter). What is the volume of metal in the hex nut, to the nearest tenth? Use 3.14 for π. 21.1 cm3 23.6 cm3 27.6 cm3 31.6 cm3

Answer 1

23.6

Explanation:

Edge 2020

Answer 2

`V=V_p-V_cV=27.712 cm^3 - 4.019 cm^3V=23.693 cm^3V=23.6 cm^3`

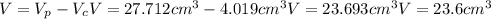
Explanation:

Given that:

Diameter of the cylinder: d=1.6 cm

Apothem of the hexagon: a=2 cm

Assuming the thickness of the steel hex nut: t=2 cm

Volume of metal in the hex nut: V=?

`V=V_p-V_c`

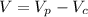
`\texttt {Volume of the prism}: V_p\\\\\texttt {Volume of the cylinder}: V_c`

Prism:

`V_p=Ab h`

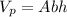
Ab=n L a / 2

Number of the sides: n=6

Side of the hexagon: L

Height of the prism: h=t=2 cm

Central angle in the hexagon: A=360°/n

A=360°/6

A=60°

`\tan (A)/(2) =(L)/(2) / a`

`\tan (60)/(2) =(L)/(2) / 2cm`

`\tan 30 =(L)/(2) / 2cm`

`(√(3) )/(3) =((L)/(2) )/(2)`

`2(√(3) )/(3) =(L)/(2)`

`L=4(√(3) )/(3)`

`Ab=n *L *(a)/(2)`

`Ab=6(4(√(3) )/(3) )(2cm)/2`

`=24(√(3) )/(3) cm^2\\\\=8√(3) cm^2`

`V_p=Ab h`

`=(8√(3) )cm^2(2cm)\\\\=16√(3) cm^3\\\\=16(1.732)cm^3\\\\=27.712cm^3`

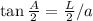
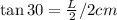
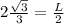
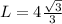
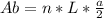
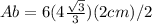
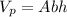
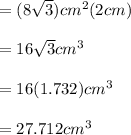
Cylinder:

`V_c=\pi(d^2)/(4) L`

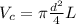
π=3.14

d=1.6 cm

Height of the cylinder: h=t=2 cm

`V_c=3.14*(1.6^2)/(4) *2\\\\=3.14*(2.56)/(4) * 2\\\\=2.0096*2\\\\=4.019cm^3`

`V=V_p-V_cV=27.712 cm^3 - 4.019 cm^3V=23.693 cm^3V=23.6 cm^3`