Question

Find the mean of the data summarized in the given frequency distribution. Compare the computed mean to the actual mean of 50.7 degrees. Low Temperature ​(circle​F) 40 minus 44 45minus49 50 minus 54 55 minus 59 60 minus 64 Frequency 2 7 9 5 1 The mean of the frequency distribution is nothing degrees. ​(Round to the nearest tenth as​ needed.)

Answer 1

51.2°F

Explanation:

Find the exact frequency table in the diagram attached. x is the midpoint of the interval f is the frequency. Using the formula below to find the mean;

`\overline x = (\sum fx)/(\sum f) \\`

`\sum fx = (42*2)+(47*7)+(52*9)+(57*5)+(62*1)\\\sum fx = 84+329+468+285+62\\\sum fx = 1,228\\\sum f = 24\\\\\overline x = (1,228)/(24) \\\overline x = 51.17^(0) F`

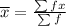
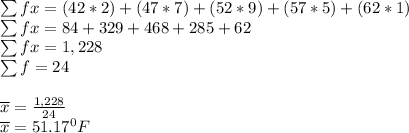
The mean of the frequency distribution compare to the actual mean of 50.7°F is 51.2°F(to nearest tenth)