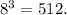- The logarithmic form of
 is
is
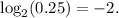
- The exponential form of
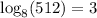 is
is
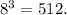
To rewrite the exponential equation
 in logarithmic form, you use the definition of a logarithm. The logarithmic form of
in logarithmic form, you use the definition of a logarithm. The logarithmic form of
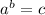 is
is
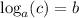 . Applying this to the given equation:
. Applying this to the given equation:
![\[ 2^(-2) = 0.25 \]](https://img.qammunity.org/2021/formulas/mathematics/college/e7zpdgn8x7pln4xps32grabntpczr99chy.png)
![\[ \log_2(0.25) = -2 \]](https://img.qammunity.org/2021/formulas/mathematics/college/qfu7hn8wzfedc6vpj7vmzwdmnu2ts32hgd.png)
This is the logarithmic form of the equation.
To rewrite the logarithmic equation
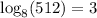 in exponential form, you use the definition of a logarithm in reverse. The exponential form of
in exponential form, you use the definition of a logarithm in reverse. The exponential form of
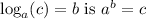 . Applying this to the given equation:
. Applying this to the given equation:
![\[ \log_8(512) = 3 \]](https://img.qammunity.org/2021/formulas/mathematics/college/nfig2h8i4vdsh08duitqg0axfm5fhd8859.png)
![\[ 8^3 = 512 \]](https://img.qammunity.org/2021/formulas/mathematics/college/69iisdb0kuq06952mvwg59vajh4dohu0pl.png)
This is the exponential form of the equation.
So, summarizing the results:
- The logarithmic form of
 is
is
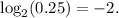
- The exponential form of
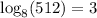 is
is