Question

Suppose a basketball player has made 184 out of 329 free throws. If the player makes the next 2 free throws, I will pay you $24. Otherwise you pay me $12. Step 1 of 2 : Find the expected value of the proposition. Round your answer to two decimal places. Losses must be expressed as negative values.

Answer 1

-.74

Explanation:

I just did the homework and this is the correct answer

Answer 2

The expected value of the proposition is -$12.74.

Explanation:

Expected value:

It is the multiplication of each outcome by it's probability.

For each free throw, there are only two possible outcomes. Either the player makes, or he does not. Each free throw is independent of each other. So we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

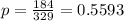
Suppose a basketball player has made 184 out of 329 free throws.

This means that
`p = (184)/(329) = 0.5593`

2 free throws:

This means that
`n = 2`

Probability of making two free throws.

This is P(X = 2).

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 2) = C_(2,2).(0.5593)^(2).(0.4407)^(0) = 0.3128`

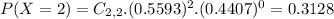
Expected value:

If he makes both free throws, you earn $12. So 0.3128 probability of you earning $12.

Otherwise, you have to pay $24. 1 - 0.3128 = 0.6872 probability of you losing $24.

So

E = 0.3128*12 - 0.6872*24 = -12.74

The expected value of the proposition is -$12.74.