Answer:
Explanation:
From the information given :
The null hypothesis
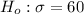
The alternative hypothesis
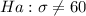
Given that:
the sample size n = 21
sample standard deviation s = 68
population standard deviation σ = 60
a) The level of significance
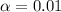
b) The chi-square statistics can be calculated as:
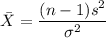
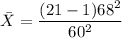
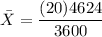
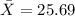
The degree of freedom is :
= n - 1
= 21 - 1
= 20