Question

About 19​% of the population of a large country is hopelessly romantic. If two people are randomly​ selected, what is the probability both are hopelessly romantic​? What is the probability at least one is hopelessly romantic​?

​(a) The probability that both will be hopelessly romantic is

0.0361.

​(Round to four decimal places as​ needed.)

​(b) The probability that at least one person is hopelessly romantic is

0.3439.

​(Round to four decimal places as​ needed.)

Answer 1

a)

The probability that both will be hopelessly romantic is

P(X = 2) = 0.0361

b)

The probability that at least one person is hopelessly romantic is

P( X>1) = 0.3439

Explanation:

a)

Given data population proportion 'p' = 19% =0.19

q = 1-p = 1- 0.19 =0.81

Given two people are randomly​ selected

Given n = 2

Let 'X' be the random variable in binomial distribution

`P(X=r) =n_{C_(r) } p^(r) q^(n-r)`

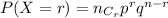
The probability that both will be hopelessly romantic is

`P(X= 2) =2_{C_(2) } (0.19)^(2) (0.81)^(2-2)`

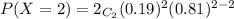
P(X = 2) = 1 × 0.0361

The probability that both will be hopelessly romantic is

P(X = 2) = 0.0361

b)

The probability that at least one person is hopelessly romantic is

P( X>1) = 1-P(x<1)

= 1 - ( p(x =0)

=
`1- 2_{C_(0) } (0.19)^(0) (0.81)^(2-0)`

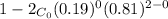
= 1 - (0.81)²

= 1 -0.6561

= 0.3439

The probability that at least one person is hopelessly romantic is

P( X>1) = 0.3439