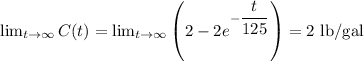Answer:
(a)
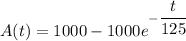
(b)
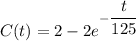
(c) C(5)=0.07842 lb/gal
(d)
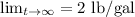
Explanation:
Amount of Salt in the Tank
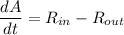
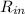 =(concentration of salt in inflow)(input rate of brine)
=(concentration of salt in inflow)(input rate of brine)
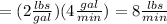
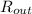 =(concentration of salt in outflow)(output rate of brine)
=(concentration of salt in outflow)(output rate of brine)
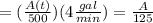
Therefore:

We then solve the resulting differential equation by separation of variables.
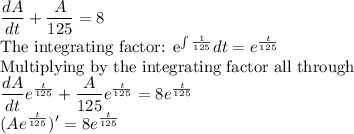
Taking the integral of both sides
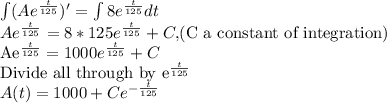
Recall that when t=0, A(t)=0 (our initial condition)
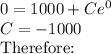
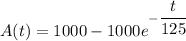
(b)
Concentration c(t) of the salt in the tank at time t
Concentration, C(t)=
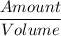
Therefore:
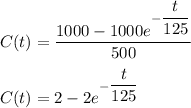
Therefore:
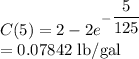
As t tends to infinity