Question

A hollow cylinder with an inner radius of 5 mm and an outer radius of 26 mm conducts a 4-A current flowing parallel to the axis of the cylinder. If the current density is uniform throughout the wire, what is the magnitude of the magnetic field at a point 12 mm from its center

Answer 1

B = 38.2μT

Step-by-step explanation:

By the Ampere's law you have that the magnetic field generated by a current, in a wire, is given by:

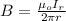`B=(\mu_o I_r)/(2\pi r)` (1)

μo: magnetic permeability of vacuum = 4π*10^-7 T/A

r: distance from the center of the cylinder, in which B is calculated

Ir: current for the distance r

In this case, you first calculate the current Ir, by using the following relation:

`I_r=JA_r`

J: current density

Ar: cross sectional area for r in the hollow cylinder

Ar is given by
`A_r=\pi(r^2-R_1^2)`

The current density is given by the total area and the total current:

`J=(I_T)/(A_T)=(I_T)/(\pi(R_2^2-R_1^2))`

R2: outer radius = 26mm = 26*10^-3 m

R1: inner radius = 5 mm = 5*10^-3 m

IT: total current = 4 A

Then, the current in the wire for a distance r is:

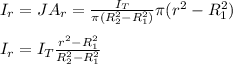`I_r=JA_r=(I_T)/(\pi(R_2^2-R_1^2))\pi(r^2-R_1^2)\\\\I_r=I_T(r^2-R_1^2)/(R_2^2-R_1^2)` (2)

You replace the last result of equation (2) into the equation (1):

`B=(\mu_oI_T)/(2\pi r)((r^2-R_1^2)/(R_2^2-R_1^2))`

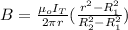
Finally. you replace the values of all parameters:

`B=((4\pi*10^(-7)T/A)(4A))/(2\PI (12*10^(-3)m))(((12*10^(-3))^2-(5*10^(-3)m)^2)/((26*10^(-3)m)^2-(5*10^(-3)m)^2))\\\\B=3.82*10^(-5)T=38.2\mu T`

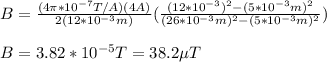
hence, the magnitude of the magnetic field at a point 12 mm from the center of the hollow cylinder, is 38.2μT