Question

Which of these relations on the set {0, 1, 2, 3} are equivalence relations? If not, please give reasons why. (In other words, if a relation is not an equivalence relation, please list each property that is missing and the reason why it is missing.) (1) {(0,0), (1,1), (2,2), (3,3)} (2) {(0,0), (0,2), (2,0), (2,2), (2,3), (3,2), (3,3)} (3) {(0,0), (1,1), (1,2), (2,1), (2,2), (3,3)} (4) {(0,0), (0,1), (0,2), (1,0), (1,1), (1,2), (2,0), (2,2), (3,3)}

Answer 1

(1)Equivalence Relation

(2)Not Transitive, (0,3) is missing

(3)Equivalence Relation

(4)Not symmetric and Not Transitive, (2,1) is not in the set

Explanation:

A set is said to be an equivalence relation if it satisfies the following conditions:

• Reflexivity: If
  `\forall x \in A, x \rightarrow x`
• Symmetry:
  `\forall x,y \in A, $if x \rightarrow y,$ then y \rightarrow x`
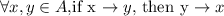
• Transitivity:
  `\forall x,y,z \in A, $if x \rightarrow y,$ and y \rightarrow z, $ then x \rightarrow z`

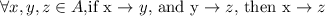
(1) {(0,0), (1,1), (2,2), (3,3)}

(3) {(0,0), (1,1), (1,2), (2,1), (2,2), (3,3)}

The relations in 1 and 3 are Reflexive, Symmetric and Transitive. Therefore (1) and (3) are equivalence relation.

(2) {(0,0), (0,2), (2,0), (2,2), (2,3), (3,2), (3,3)}

In (2), (0,2) and (2,3) are in the set but (0,3) is not in the set.

Therefore, It is not transitive.

As a result, the set (2) is not an equivalence relation.

(4) {(0,0), (0,1), (0,2), (1,0), (1,1), (1,2), (2,0), (2,2), (3,3)}

(1,2) is in the set but (2,1) is not in the set, therefore it is not symmetric

Also, (2,0) and (0,1) is in the set, but (2,1) is not, rendering the condition for transitivity invalid.