Answer:
The distance between P and Q is 54
Explanation:
We are given that triangle RPQ is similar to triangle RTS.
Property of similar triangle: The ratio of any pair of corresponding sides is the same.
So, by property :
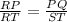
PR=42
PQ=x
ST=36
RT=28
So,
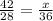
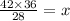
54=x
Hence the distance between P and Q is 54