Question

Jason and his brother each have the equal probability of being randomly selected to wash dishes after dinner. Jason wants to simulate the probability that more than 4 evenings will go by without him having to wash the dishes after dinner. He decides to conduct a simulation by flipping a quarter, with heads representing an evening where he washes dishes after dinner and tails representing an evening of not doing dishes after dinner. He keeps flipping until he flips heads and records the number of flips that were needed. For example, if two flips are needed to get heads, this indicates that he washes dishes on the second evening. He repeats this 50 times and records the data on the table below Number of flips until getting heads: 1,2,3,4,5,6,7,8 frequency: 21,18,4,4,2,0,0,1 Based on the results of the simulation, what is the probability that more than 4 evenings will go by without Jason having to wash dishes after dinner? [blank] %

Answer 1

The probability that more than 4 evenings will go by without Jason having to wash dishes after dinner is 0.06.

Explanation:

We are given that Jason wants to simulate the probability that more than 4 evenings will go by without him having to wash the dishes after dinner.

He repeats this 50 times and records the data on the table below;

Number of flips until getting heads Frequency

1 21

2 18

3 4

4 4

5 2

6 0

7 0

8 1

Total 50

Now, we have to find the probability that more than 4 evenings will go by without Jason having to wash dishes after dinner.

This will happen only when the Number of flips until getting heads is 5, 6, 7 or 8 as only then Jason will have more than 4 evenings go by without washing dishes after dinner.

So, required probability =
`(2)/(50)+(0)/(50)+(0)/(50)+(1)/(50)`

=
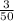`(3)/(50)` = 0.06