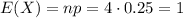Question

Some parts of California are particularly earthquake- prone. Suppose that in one metropolitan area, 25% of all homeowners are insured against earthquake damage. Four homeowners are to be selected at random; let X denote the number among the four who have earthquake insurance. a. Find the probability distribution of X. [Hint: Let S denote a homeowner who has insurance and F one who does not. Then one possible outcome is SFSS, with proba bility (.25)(.75)(.25)(.25) and associated X value 3. There are 15 other outcomes.] b. Draw the corresponding probability histogram. c. What is the most likely value for X

Answer 1

a. Binomial random variable (n=4, p=0.25)

b. Attached.

c. X=1

Explanation:

This can be modeled as a binomial random variable, with parameters n=4 (size of the sample) and p=0.25 (proportion of homeowners that are insured against earthquake damage).

a. The probability that X=k homeowners, from the sample of 4, have eartquake insurance is:

`P(x=k) = \dbinom{n}{k} p^(k)(1-p)^(n-k)\\\\\\P(x=k) = \dbinom{4}{k} 0.25^(0)\cdot0.75^(4)`

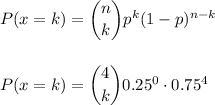
The sample space for X is {0,1,2,3,4}

The associated probabilties are:

`P(x=0) = \dbinom{4}{0} p^(0)(1-p)^(4)=1*1*0.3164=0.3164\\\\\\P(x=1) = \dbinom{4}{1} p^(1)(1-p)^(3)=4*0.25*0.4219=0.4219\\\\\\P(x=2) = \dbinom{4}{2} p^(2)(1-p)^(2)=6*0.0625*0.5625=0.2109\\\\\\P(x=3) = \dbinom{4}{3} p^(3)(1-p)^(1)=4*0.0156*0.75=0.0469\\\\\\P(x=4) = \dbinom{4}{4} p^(4)(1-p)^(0)=1*0.0039*1=0.0039\\\\\\`

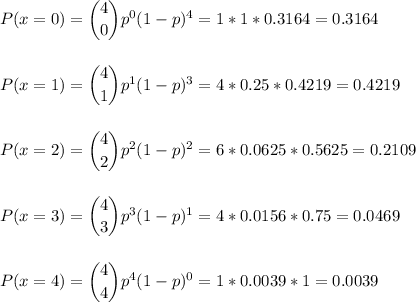
b. The histogram is attached.

c. The most likely value for X is the expected value for X (E(X)).

Is calculated as:

`E(X)=np=4\cdot0.25=1`