Question

Automobile policies are separated into two groups: low-risk and high-risk. Actuary Rahul examines low-risk policies, connuing unl a policy with a claim is found and then stopping. Actuary Toby follows the same procedure with high-risk policies. Each low-risk policy has a 10% probability of having a claim. Each high-risk policy has a 20% probability of having a claim. The claim statuses of polices are mutually independent. Calculate the probability that Actuary Rahul examines fewer policies than Actuary Toby.

Answer 1

The probability that Actuary Rahul examines fewer policies that Actuary Toby = 0.2857

Explanation:

It is said that Actuary Rahul examines a low risk policy

Probability of a low risk policy having a claim = 10% = 0.1

Actuary Toby examines high risk policy

Probability of a high risk policy having a claim = 20% = 0.2

Let the number of policies examined by actuary Rahul before he finds a claim and stop be n

Probability that actuary Rahul examines exactly n policies =
`0.9^(n-1) (0.1)`

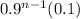
Probability that Toby examines more than n policies =
`0.8^n`

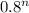
Since the claim statuses of policies are mutually independent, the probability that both events happen simultaneously =
`0.9^(n-1) (0.1) (0.8)^n`

probability that both events happen simultaneously =
`(0.1)/(0.9) (0.72^(n))`

The probability that Actuary Rahul examines fewer policies that Actuary Toby =
`\sum\limits^ \infty_1 {(0.1)/(0.9) 0.72^(n) }` =
`(1)/(9)\sum\limits^ \infty_1 { 0.72^(n) } = (1)/(9) ((0.72)/(1-0.72) ) = (1)/(9) ((0.72)/(0.28) )`

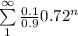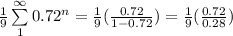
The probability that Actuary Rahul examines fewer policies that Actuary Toby = 0.2857