Question

Each have four possible answers left parenthesis a,b,c,d right parenthesis​, one of which is correct. Assume that you guess the answers to three such questions.

a. Use the multiplication rule to find ​P(CWC​), where C denotes a correct answer and W denotes a wrong answer.
b. Beginning with CWC​, make a complete list of the different possible arrangements of two correct answers and one wrong answer​, then find the probability for each entry in the list.​P(CWC​)minussee above ​P(WCC​)equals? 0.046875 ​P(CCW​)equals? 0.046875 ​(Type exact​ answers.)
c. Based on the preceding​ results, what is the probability of getting exactly two correct answers when three guesses are​made?

Answer 1

a. P(CWC)=0.046875

b. P(WCC)=0.046875

P(CCW)=0.046875

c. P=0.140625

Explanation:

By the rule of multiplication there are 64 forms to answer three questions. This is calculated as:

4 _ * 4 * 4 = 64

1st question 2nd question 3rd question

Because there are 4 options for every question. At the same way, from that 64 options, 3 are CWC and it is calculated as:

1 _ * 3 * 1 = 3

1st question 2nd question 3rd question

Because there is just one answer that is correct for the first question, there are 3 answers wrong for the second question and there are 1 answer correct for the third question.

So, the probability P(CWC) is equal to:

`P(CWC)=(3)/(64)=0.046875`

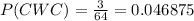
Then, the complete list of the different possible arrangements of two correct answers and one wrong answer are: CWC, WCC and CCW

Therefore, the probabilities P(WCC) and P(CCW) are calculated as:

`P(WCC)=(3*1*1)/(64)=(3)/(4)= 0.046875`

`P(CCW)=(1*1*3)/(64)=(3)/(4)= 0.046875`

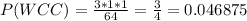
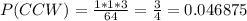
Finally, the probability of getting exactly two correct answers is the sum of the probabilities calculated before.

`P=P(CWC)+P(WCC)+P(CCW)\\P=0.046875+0.046875+0.046875\\P=0.140625`