The problem wishes us to integrate
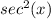
-However, we know based on the derivation of tan (x)

Bascially integration is the reversal of the derivation:
Thus
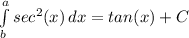
Since there are no bounds, we must add a constant 'C' as we don't know if there was an initial value
Hope that helps!