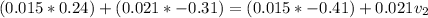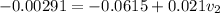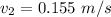Question

A 15 g toy car moving to the right at 24 cm/s has a head-on nearly elastic collision with a 21 g toy car moving in the opposite direction at 31 cm/s. After colliding, the 15 g car moves with a velocity of 41 cm/s to the left. Find the speed of the second car after the collision.

Answer 1

The speed of the second toy car after collision is
`v_2 = 0.155 \ m/s`

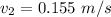
Step-by-step explanation:

Let movement to the right be positive and the opposite negative

From the question we are told that

The mass of the car is
`m_1 = 15 \ g = (15)/(1000) = 0.015 \ kg`

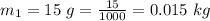
The initial velocity of the car is
`u_1 = 24 \ cm /s = 0.24 m/s`

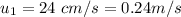
The mass of the second toy car
`m_2 = 21 g = 0.021 \ kg`

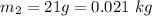
The initial velocity of the car is
`u_2 = 31 \ cm/s =- 0.31 m/s`

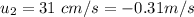
The final velocity of the first car is
`v = 41cm/s = - 0.41 m/s`

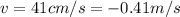
From law of momentum conservation we have that

`m_1 u_1 + m_2 u_2 = m_1 v_1 + m_2 v_2`

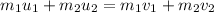
substituting values

`(0.015* 0.24) +( 0.021 * -0.31) = (0.015 * -0.41 ) + 0.021 v_2`

`-0.00291 = -0.0615 + 0.021 v_2`

`v_2 = 0.155 \ m/s`