Question

Determine whether b can be written as a linear combination of Bold a Subscript Bold 1a1​, Bold a Subscript Bold 2a2​, and Bold a Subscript Bold 3a3. In other​ words, determine whether weights x 1x1​, x 2x2​, and x 3x3 ​exist, such that x 1x1Bold a Subscript Bold 1a1plus+x 2x2Bold a Subscript Bold 2a2plus+x 3x3Bold a Subscript Bold 3a3equals=b. Determine the weights x 1x1​, x 2x2​, and x 3x3 if possible.

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

a

b can be written as a linear combination of
`a_1 \ and \ a_2`

b

The values of
`x_1 = 4 \ and \ x_2 = 2`

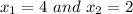
Explanation:

From the question we are told that

`x_1 a_1 +x_2 a_2 = b`

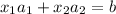
Where
`a_ 1 = (4, 5,-4)`,
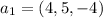`a_2 = (-4 , 3, 3)` and
`b = (8,26 , -10)`

So

`x_1 ( 4, 5,-4) + x_2 (-4 , 3, 3) = (8,26 , -10)`

`4x_1, 5x_1,-4x_1 + -4x_2 , 3x_2, 3x_2 = (8,26 , -10)`

=>
`4x_1 -4x_2 =8`

`x_1 -x_2 =2 ---(1)`

=>
`5x_1 + 3x_2 = 26 --- (2)`

=>
`-4x_1 + 3x_2 = -10 ---(3)`

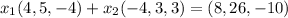
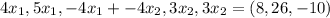
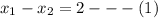
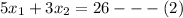
Now multiplying equation 1 by 3 and adding the product to equation 2

`.\ \ \ 3x_1 -3x_2 = 6\\+ \ \ 5x_1 + 3x_2 = 26 \\=> \ \ \ 8x_1 = 32`

=>
`x_1 = 4`

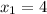
substituting
`x_1` into equation 1

`4 - x_2 =2`

`x_2 =2`

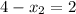
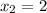
Now to test substitute
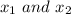`x_1 \ and \ x_2` into equation 3

`-4(4) + 3(2) = -10`

`-10 = -10`

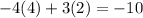
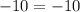
Since LHS = RHS then there exist values
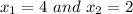`x_1 = 4 \ and \ x_2 = 2` such that

`x_1 a_1 +x_2 a_2 = b`

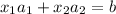
Hence b can be written as a linear combination of
`a_1 \ and \ a_2`