Answer:
Hence, the system of equation does not have solution.
Explanation:
You have the following 2x2 system:
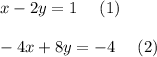
You can obtain the solution to the system by using substitution method.
You solve the first equation for x:
 (3)
(3)
Next, you replace (3) in the equation (2), and you solve for y:

The last result is the trivial solution. This means that the equation (2) is a multiple scale of the first equation. In fact, if you multiply equation (1) by -4, you obtain the equation (2).
Hence, the system of equations does not have solution.