Question

An urn contains 9 red marbles, 9 white marbles and 8 blue marbles. A child randomly selects three (without replacement).

what is the probability that all have the same color?

Answer 1

8.62% probability that all have the same color

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

The order in which the marbles are selected is not important. So we use the combinations formula to solve this question.

Combinations formula:

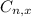`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

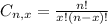
What is the probability that all have the same color?

Desired outcomes:

Either all red(from a set of 9), all white(from a set of 9) or all blue(from a set of 8). So

`D = C_(9,3) + C_(9,3) + C_(8,3) = (9!)/(3!6!) + (9!)/(3!6!) + (8!)/(3!5!) = 224`

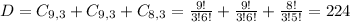
Total outcomes:

3 marbles, from a set of 9 + 9 + 8 = 26. So

`T = C_(26,3) = (26!)/(3!23!) = 2600`

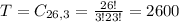
Probability:

`p = (D)/(T) = (224)/(2600) = 0.0862`

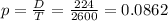
8.62% probability that all have the same color