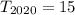Question

Explain in detail, how you solved the following problem: The first two terms of a sequence are 10 and 20. If each term after the second term is the average of all of the preceding terms, what is the 2020th term?

Answer 1

`T_(2020) = 15`

Step-by-step explanation:

Given

`T_1 = 10`

`T_2 = 20`

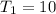
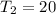
Each term after the second term is the average of all of the preceding terms

Required:

Explain how to solve the 2020th term

Solve the 2020th term

Solving the 2020th term of a sequence using conventional method may be a little bit difficult but in questions like this, it's not.

The very first thing to do is to solve for the third term;

The value of the third term is the value of every other term after the second term of the sequence; So, what I'll do is that I'll assign the value of the third term to the 2020th term

This is proved as follows;

From the question, we have that "..... each term after the second term is the average of all of the preceding terms", in other words the MEAN

`T_(n) = \frac{\sum T{k}}{n-1} ; where: k = 1 .... n -1`

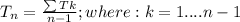
Assume n = 3

`T_(3) = (T_1 + T_2)/(2)`

Multiply both sides by 2

`2 * T_(3) = (T_1 + T_2)/(2) * 2`

`2T_(3) = T_1 + T_2`

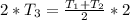
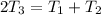
Assume n = 4

`T_(4) = (T_1 + T_2 + T_3)/(3)`

`T_(4) = ((T_1 + T_2) + T_3)/(3)`

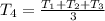
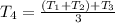
Substitute
`2T_(3) = T_1 + T_2`

`T_(4) = (2T_3 + T_3)/(3)`

`T_(4) = (3T_3)/(3)`

`T_(4) = T_3`

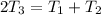
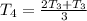
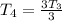
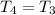
Assume n = 5

`T_(5) = (T_1 + T_2 + T_3 +T_4)/(4)`

`T_(5) = ((T_1 + T_2) + T_3 +(T_4))/(4)`

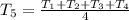
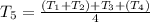
Substitute
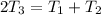`2T_(3) = T_1 + T_2` and
`T_(4) = T_3`

`T_(5) = (2T_3 + T_3 +T_3)/(4)`

`T_(5) = (4T_3)/(4)`

`T_(5) = ((5-1)T_3)/(5-1)`

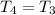
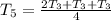
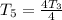
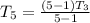
Replace 5 with n

`T_(n) = ((n-1)T_3)/(n-1)`

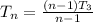
(n-1) will definitely cancel out (n-1); So, we're left with

`T_(n) = T_3`

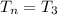
Hence,

`T_(2020) = T_3`

Calculating
`T_3`

`T_(3) = (10 + 20)/(2)`

`T_(3) = (30)/(2)`

`T_(3) = 15`

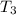
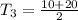
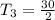
Recall that
`T_(2020) = T_3`

`T_(2020) = 15`