Question

Two fans are watching a baseball game from different positions. One fan is located directly behind home plate, 18.3 mfrom the batter. The other fan is located in the centerfield bleachers, 127 m from the batter. Both fans observe the batterstrike the ball at the same time(because the speed of light is about a million times faster than that of sound), but the fan behind home plate hears the sound first. What is the time difference between hearing the sound at the two locations? Use 345 m/s as the speed of sound.

Answer 1

Δt = 0.315s

Step-by-step explanation:

To calculate the time difference, in which both fans hear the batterstrike, you first calculate the time which takes the sound to travel the distances to both fans:

`t_1=(d_1)/(v_s)`

`t_2=(d_2)/(v_s)`

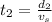
d1: distance to the first fan = 18.3 m

d2: distance to the second fan = 127 m

vs: speed of sound = 345 m/s

You replace the values of the parameters to calculate t1 and t2:

`t_1=(18.3m)/(345m/s)=0.053s\\\\t_2=(127m)/(345m/s)=0.368s`

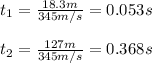
The difference in time will be:

`\Delta t =t_2-t_2=0.368s-0.053s=0.315s`

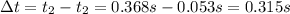
Hence, the time difference between hearing the sound at the location s of both fans is 0.315s